
More Helpful Content
Nowadays, manufacturing businesses calculate the quantity of every material required for production and when it is needed using a technique called "Material Requirements Planning."
The order's size must be determined by the material planner, who is also responsible for placing it. Placing many orders each month might be highly expensive, not to mention the costs associated with keeping inventory on hand.
They should decide how best to balance the costs in order to come up with a viable financial solution.
The "lot sizing" optimization problem is thus named. In this article, we will discuss one technique of lot sizing: the least unit cost technique and example to help you have a better understanding.

The Least Unit Cost or LUC approach is a dynamic lot-sizing sizing strategy that determines the order quantity by identifying whether or not the demand for the following "n" periods, where "n" reduces the average cost per unit, will be met.
LUC is used to take the advantage of economic purchase discounts and also to meet the variations in the product demand
👉 Read More: What is the planned order release? Formula and Example
👉 Read More: What Is the Cost of Goods Sold (COGS)? Formula and Examples
👉 Read More: What Is Dead Stock In Inventory Management?
The Least Unit Cost approach seeks to reduce the average cost per unit. One piece of machinery, raw material, or component is referred to as a unit.
When "n" is chosen to minimize the average cost per unit, we determine the order quantity that will span the following "n" periods.
The Least Unit Cost approach is a dynamic lot-sizing technique that multiplies each test lot size's ordering and inventories carrying costs by the quantity of units in every lot size, then chooses the test lot size with the smallest unit cost.
In this example, we'll apply a new table to this technique's computation of the best lot size.
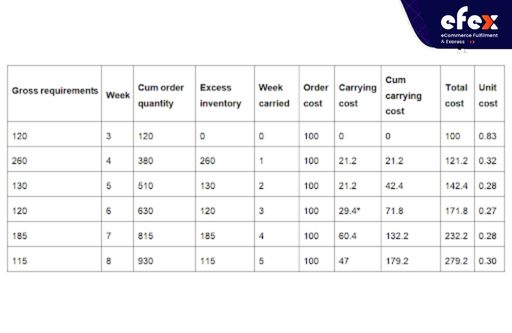
Cumulative order quantity: the total amount to be ordered per week
Excessive inventory is that which is not required now but will be in the future.
Week carried: The total number of weeks that the extra inventory is carried.
👉 Read More: What Is Kitting In Manufacturing: Process and Benefits
Since the cost per unit would be 0.27 euros each week in the instance below, the LUT technique would advise ordering 630 units, which would satisfy the anticipated demand until week 6.
After the week 6, when we have a better understanding of the anticipated demand for the following few weeks, we re-start the process.
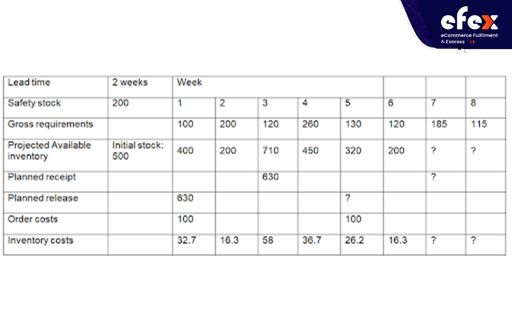
Order price: 200 Euros
Inventory costs: 186.2€ plus (unknown for the previous two periods)
Costs of purchases: (630 +?)*25€ = ?
Entire cost: To estimate the total cost, we need to know the requirements for the upcoming time periods.
We should execute the following example, also adhering to the presentation and formulas in Silver et al (1998) and Nahmias (2013)
Cost if only the necessary quantity is ordered during Period 1:
Cost for obtaining the following required amount in period 2 as well:
Cost for ordering period 3's zero requested quantity as well:
The preceding Least Unit Cost is unaffected by a zero demand, hence the search goes on.
Cost for ordering the third quantity that was requested after period 6:
0.88 > 0.85; therefore Q1=t=14Xt=t=13Xi, ti= 100 +100+ 200 = 400 units
Therefore, starting in period 5 makes no sense in order to compute the required order quantity for the subsequent order quantity, which we start in period 6 instead.
Cost for ordering the quantity in the period 6: A/X4,t4=200/100=2 MU/ unit
Cost of ordering the additional quantity in period 8 in addition to the quantity required in period 6:
Therefore, Q2=t=69Xt=t=45Xi, ti= 100 +350=450 units
This response provides the entire cost of setup and inventory holding:
👉 Read More: Order Management System: Definition, Process And Value
👉 Read More: Order Management System For Ecommerce: Definition, Key Effect, Benefit
To make finished goods, manufacturing companies need to buy a lot of raw materials and base components, the majority of which are supplied by outside vendors.
The least unit cost technique is the way to optimize the balance between the costs to find a viable financial solution.
We hope this post has already been useful for you. Feel free to ask us if you still have questions about the least unit cost.


